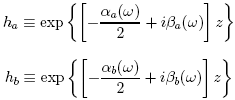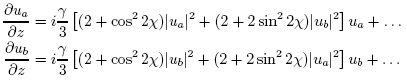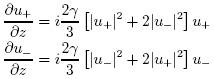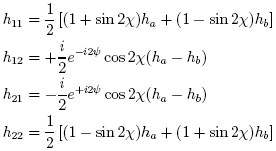Background
The vector version of the SSPROP solves the coupled nonlinear Schrödinger equations for propagation in a birefringent fiber. The code can model birefringence, differential group delay (PMD), polarization-dependent dispersion, and polarization dependent loss, all in the context of nonlinear propagation.
The user may choose from two different algorithms, depending on whether the birefringent beat length is shorter or longer than the nonlinear length.
Birefringence
In general, the birefringent axes of an optical fiber may not be oriented in the x- and y- directions, but in some other arbitrary direction ψ. Moreover, the two orthogonal eigenstates of the fiber may not even be linearly polarized — they could be circularly or even elliptically polarized. This would be the case, for example, in fiber that is twisted or spun during or after fabrication. To handle the most general case, SSPROP allows the user to separately specify not only the dispersion β(ω) and loss (α) for each of the two eigenstates, but also the exact polarization states to which these coefficients apply.
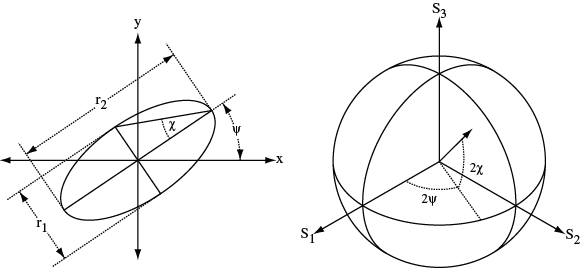
The most general elliptical polarization state can be described by two angular parameters, ψ and χ. As depicted in the figure below, ψdescribes the angle that the polarization ellipse makes with the x-axis and χ is an anglar quantity that describes the degree of ellipticity.
Positive values of χ correspond to right-handed polarization states while negative values of χ are left-handed polarization states. χ = 0 corresponds to linear polarization while χ = π/4 is circularly polarized. On the Poincaré sphere, 2ψ and 2χ describe the longitude and lattitude of the principal eigenstate, respectively.
When specifying the eigenstates of the fiber, it is sufficient to give ψ and χ for one eigenstate because the second eigenstate is known to be orthogonal to the first.
Elliptical Basis Method
Any polarization state may be decomposed into a linear combination of the two orthogonal eigenstates of the fiber, which we label “a” and “b”. If ux and ux represent the two components of the electric field vector in the x-y basis (i.e., the Jones vector), then the corresponding components ua and ub can be calculated using the unitary transformation:
where ψ and χ describe the principal eigenstate (“a”) of the fiber. In this new basis, the linear portion of the wave equations for ua and ub are decoupled. The linear portion of the propagation can therefore be performed separately on ua and ub in the spectral domain, using a technique analogous to that used in the scalar case.
where ha and hb are given by:
When performing the nonlinear part of the propagation, the appropriate coupled nonlinear equations (with linear terms omitted) are [Menyuk, JQE 1989]:
where χ quantifies the degree of ellipticity of the eigenstates as described above. The (…) terms in the above expression denote additional nonlinear terms that average to zero when the birefringent beat length is much shorter than the nonlinear length. These additional terms are also identically zero when the eigenstates are circularly polarized.
After propagating through the desired number of steps, the final solution can be rotated from the elliptical basis (ua, ua) back into the Jones basis (ux,uy) by using the inverse transformation:
Circular Basis Method
When the fiber birefringence is small, i.e., when the beat length is comparable to or larger than the nonlinear length, the additional terms in the nonlinear equations cannot be neglected. In this case, it is necessary to decompose the field into left- and right-hand circular polarization components before computing the nonlinear propagation. The circular components u+ and u– can be computed from ux and uy using the following unitary transformation:
With this transformation, the coupled nonlinear equations for u+ and u– become (again omitting linear terms):
where in this case no additional nonlinear terms have been neglected. Because the eigenstates of the fiber are not in general circularly polarized, the linear portion of the propagation is not as simple in the circular basis. After some algebra, one finds that the linear propagation can be be computed in the spectral domain, using the following matrix multiplication:
where the matrix elements hnm are given by:
and ha and hb are the same quantities given earlier in the context of the elliptical basis method.
After propagating through the desired number of steps, the final solution can be rotated from the circular basis (u+, u–) back into the Jones basis (ux,uy) by using the inverse transformation:
The circular basis method is more accurate than the elliptical basis method because it does not neglect any nonlinear terms. The disadvantage of the circular method is that the stepsize dz must always be much smaller than the beat length in order to produce meaningful results. If the beat length is smaller than the nonlinear length, this requirement forces one to use a stepsize that is much smaller than the nonlinearity would otherwise dictate.
Syntax
A summary of the syntax and usage can be obtained from Matlab by typing “help sspropv” or “help sspropvc“.
The compiled mex file (sspropvc) can be invoked from Matlab using one of the following forms:
u1 = sspropvc(u0x,u0y,dt,dz,nz,alphaa,alphab,betapa,betapb,gamma);
u1 = sspropvc(u0x,u0y,dt,dz,nz,alphaa,alphab,betapa,betapb,gamma,psp,method);
u1 = sspropvc(u0x,u0y,dt,dz,nz,alphaa,alphab,betapa,betapb,gamma,psp,method,maxiter);
u1 = sspropvc(u0x,u0y,dt,dz,nz,alphaa,alphab,betapa,betapb,gamma,psp,method,maxiter,tol);
The last four arguments assume a default value if they are left unspecified. The corresponding Matlab m-file can be invoked using a similar syntax by replacing sspropvc with sspropv.
sspropvc may also be invoked with a single input argument, to specify options specific to the FFTW routines (discussed below):
sspropvc -option
Input Arguments
|
u0x, u0y
|
vector (N) | Input optical field, specified by two length-N vector time sequences. u0x represents the x-component of the complex, slowly-varying envelope of the optical field, and u0y represents the corresponding y-component. The fields should be normalized so that |u0x|^2 + |u0y|^2 is the optical power. |
| dt | scalar | The time increment between adjacent points in the vector u0. |
| dz | scalar | The step-size to use for propagation |
| nz | scalar (int) | The number of steps to take. The total distance propagated is therefore L = nz*dz |
| alphaa, alphab | scalar or vector (N) | The linear power attenuation coefficients for the two eigenstates of the fiber. Here we use the labels “a” and “b” to denote the two eigenstates, which need not coincide with the x-y axes. Polarization dependent loss is modeled by using different numbers for alphaa and alphab.The loss coefficient may optionally be specified as a vector of the same length as u0x, in which case it will be treated as vector that describes a wavelength-dependent loss coefficient α(ω) in the frequency domain. (The function wspace.m in the tools subdirectory can be used to construct a vector with the corresponding frequencies.) |
| betapa, betapb | vector | Real-valued vectors that specify the dispersion for each eigenstate (a, b) of the fiber. The dispersion can be specified to any polynomial order by using a betap vector of the appropriate length.Birefringence is accomodated by making the first elements betapa(1) and betapb(1) unequal. Differential group delay, or polarization mode dispersion is likewise treated by making the second elements betapa(2) and betapb(2) different. (See note below for a more complete discussion.)The propagation constant can also be specified directly by replacing the polynomial argument betap with a vector of the same length as u0x. In this case, the argument betap is treated as a vector describing propagation constant β(ω) in the frequency domain. (The function wspace.m in the tools subdirectory can be used to construct a vector with the corresponding frequencies.) |
| gamma | scalar | A real number that describes the nonlinear coefficient of the fiber, which is related to the mode effective area and the nonlinear refractive index n2. |
| psp | scalar or vector (2) | Principal eigenstate of the fiber, specified as a 2-vector containing the angles ψ and χ (see discussion above), psp = [ψ ,χ].If psp is a scalar, it is interpreted to be ψ, and χ is then taken to be zero. This corresponds to a linearly-birefringent fiber whose axes are oriented at an angle χ with respect to the x-y axes.If psp is left completely unspecified, it assumes a default value of [0,0], which means that the fiber eigenstates are linearly polarized along the x- and y- directions. |
| method | string | String that specifies which method to use when performing the split-step calculations. The following methods are recognized “elliptical” or “circular”.When method = “elliptical”, sspropv will solve the equations by decomposing the input field into the (in general) elliptical eigenstates of the fiber. This method is appropriate only in fibers where the birefringent beat length is much shorter than the nonlinear length.When method = “circular”, sspropv will instead solve the equations by decomposing the input field into a right- and left-circular basis. This method is more accurate, but requires that the step size be small compared to the beat length. |
| maxiter | scalar (int) | The maximum number of iterations to make per step. If the solution does not converge to the desired tolerance within this number of iterations, a warning message will be generated. Usually this means that the chosen stepsize was too small. (default = 4) |
| tol | scalar | Convergence tolerance: controls to what level the solution must converge when performing the symmetrized split-step iterations in each step. (default = 10–5.) |
Output Arguments
|
u1x, u1y
|
vector (N) | Output optical field, specified as two length-N vectors. |
Options
Several internal options of the routine can be controlled by separately invoking sspropvc with a single argument:
sspropvc -savewisdom
sspropvc -forgetwisdom
sspropvc -loadwisdom
The first command will save the accumulated FFTW wisdom to a file that can be later used. The second command causes sspropc to forget all of the accumulated wisdom. The last command forces FFTW to load the wisdom file from the current directory. The wisdom file (if it exists) is automatically loaded the first time sspropvc is executed. The name of the wisdom file is “fftw-wisdom.dat” for the double-precision version of the program and “fftwf-wisdom.dat” for the single-precision version. This can be changed by recompiling the code. The wisdom files can and are shared between the vector and scalar versions of SSPROP. Note that the wisdom files are platform- and machine-specific. You should not expect optimal performance if you use wisdom files that were generated on a different computer.
The following four commands can be used to designate the planner method used by the FFTW routines in subsequent calls to sspropc.
sspropvc -estimate
sspropvc -measure
sspropvc -patient
sspropvc -exhaustive
The default method is patient. These settings are reset when the function is cleared or when Matlab is restarted.
These options are only available in the compiled version of the routine.
Notes
Slowly-varying Envelope: In the scalar version of SSPROP, is is customary to factor out the rapidly oscillating terms exp(i(β0z – ωt)) from the field in order to obtain an equation for the slowly-varying envelope. In SSPROP, this is achieved by setting the first argument of the dispersion polynomial betap(1) equal to 0. In a fiber that has birefringence, it is no longer clear how to factor out these rapid oscillations: should we use β0x or β0y? One approach is to factor out exp(iβ0xz) from the x-component of the field and exp(iβ0yz) from the y-component of the field. However, with this definition we can no longer regard u0x and u0y as a Jones vector that describes the polarization state. Therefore, we instead choose to factor out a common phase exp(iβ0avgz) variation from both components of the field. Provided we choose β0avg to be the average of β0x and β0y, the resulting fields ux and uy will still be slowly-varying envelopes that describe the instantaneous Jones vector of the optical signal. In SSPROP, this is accomplished numerically by choosing betapa(1) and betapb(1) to be equal and opposite such that betapa(1) – betapb(1) = Δβ0.
Moving Reference Frames: A similar consideration applies to the difference in group velocity. In a birefringent fiber, the group velocities can be different for the x- and y- polarizations. Therefore we solve the nonlinear Schrodinger equations in a reference frame that is moving at a velocity in between vx and vy. This amounts to making a change of varibles T = t – β1avgz, where β1avg is the average value of β1. In SSPROP, this is accomplished numerically by choosing betapa(2) and betapb(2) to be equal and opposite such that betapa(2) – betapb(2) = Δβ1.
Units and Dimensions: The dimensions of the input and output quantities are arbitrary, as long as they are self consistent. For examle, if |u0|2 has dimensions of Watts and dz has dimensions of meters, then the nonlinearity parameter gamma should be specified in W-1m-1. Similarly, if dt is given in picoseconds, and dz is given in meters, then the dispersion polynomial coefficients betap(n) should have dimensions of ps(n-1)/m. It is of course possible to solve the normalized dimensionless nonlinear Schrödinger equation by setting some of the input terms to 1 or –1 as appropriate.
Periodicity: SSPROP uses the FFT (DFT) to calculate the spectrum, which implies that the input and output signals are periodic in time. The periodicity is determined by the time increment and the length of the input vector, T = dt*length(u0x). Because of the periodic boundary conditions used by the DFT, care must be taken to ensure that if the optical field at the edges of the window is not negligible it must be continuous in both magnitude and phase.
Iterations and Tolerance: The last two optional parameters, maxiter and tol are related to the symmetrized split-step iteration algorithm. The algorithm uses a trapazoid integration equation to approximate the effect of the nonlinearity over a distance dz, but this approximation requires knowledge of the field at the subsequent distance-step. This problem is solved by using an iterative approach. maxiter represents the maximum number of iterations performed per step, and tol is a positive dimensionless number that tells the algorithm what level of convergence is required before the iteration stops.