Published/Posted: July 22, 2015
Authors: Hagerstrom, A. M.
DOI: 10.13016/M23S8J
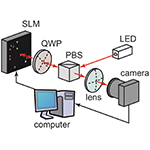
Abstract: This thesis describes work in two areas: unpredictability in a system with both single photon detection and chaos, and synchronization in networks of coupled systems. The unpredictability of physical systems can depend on the scale at which they are observed. For example, single photons incident on a detector arrive at random times, but slow intensity variations can be observed by counting many photons over large time windows. We describe an experiment in which a weak optical signal is modulated by feedback from a single-photon detector. We demonstrate that at low photon rates, the photon arrivals are described by Poisson noise, while at high photon rates, the intensity of the light shows a deterministic chaotic modulation. Furthermore, we show that measurements of the entropy rate can resolve both noise and chaos, and describe the relevance of this observation to random number generation. We also describe an experimental system that allows for the study of large networks of coupled dynamical systems. This system uses a spatial light modulator (SLM) and a camera in a feedback configuration, and has an optical nonlinearity due to the relationship between a spatially-dependent phase shift applied by the modulator, and the intensity measured by the camera. This system is a powerful platform for studying synchronization in large networks of coupled systems, because it can iterate many (~1000) maps in parallel, and can be configured with any desired coupling matrix. We use this system to study cluster synchronization. It is often observed that networks synchronize in clusters. We show that the clusters that form can be predicted based on the symmetries of the network, and their stability can be analyzed. This analysis is supported by experimental measurements. The SLM feedback system can also exhibit chimera states. These states were first seen in models of large populations of coupled phase oscillators. Their defining feature is the coexistence of large populations of synchronized and unsynchronized oscillators in spite of symmetrical coupling configurations and homogeneous oscillators. Our SLM feedback system provided one of the first two experimental examples of chimera states. We observed chimeras in coupled map lattices. These states evolve in discrete time, and in this context, ``coherence'' and ``incoherence'' refer to smooth and discontinuous regions of a spatial pattern.Citation:
A. M. Hagerstrom, "Experimental study of entropy generation and synchronization in networks of coupled dynamical systems", PhD Physics, University of Maryland (2015)
Manuscript: Hagerstrom_PhD_Thesis_2015.pdf